Inleiding
Op deze pagina lees je hoe je wiskundige formules korter kunt schrijven door haakjes weg te werken en gelijksoortige termen samen te nemen. De groene knop brengt je naar de oefenopgaves.
De letter als plaatshouder voor een getal
In de wiskunde is het heel normaal om letters te gebruiken op plaatsen waar je een cijfer kunt gebruiken. Door een letter te gebruiken zeg je eigenlijk: “Op deze plek mag elk getal komen te staan”. Dat is heel handig als je een formule opschrijft.
Stel dat je 7,50 zakgeld per week krijgt, dan heb je na één maand 30,00 gespaard. Namelijk 4 x 7,50. Je spaargeld is dus gelijk aan het aantal weken dat je spaart, vermenigvuldigd met 7,50.
Hier kunnen we een formule van maken: aantal weken x 7,50 = spaargeld of kortweg a x 7,50 = s.
In deze formule staan twee letters a en s. Beide letters stellen getallen voor. Door de a te vervangen voor een willekeurig getal kan je het spaargeld s uitrekenen. Vervang je de a door 10, dan wordt je spaargeld 10 x 7,50 = 75,00.
De letter als veranderlijke
Je kunt uit de zakgeldformule ook concluderen dat je spaargeld verandert als a veranderd. Je spaargeld hangt dus af van het aantal weken dat je spaart. Hoe langer je spaart, hoe rijker je wordt.
Basisregel 1
Het “x” teken tussen een letter en een getal schrijven we niet op. We schrijven eerst het cijfer, en dan de letter.
Basisregel 2
Gelijksoortige termen tellen we bij elkaar op (samen nemen) Let daarbij goed op de “+” en “-“ tekens
Basisregel 3
De “1” voor een letter schrijven we niet op
De tegeltjes methode
De onderstaande rechthoek is d.m.v. een stippellijn verdeelt is twee stukken. De oppervlakte van de groene rechthoek is de som van de oppervlakte van rechthoek I en de oppervlakte van rechthoek II.
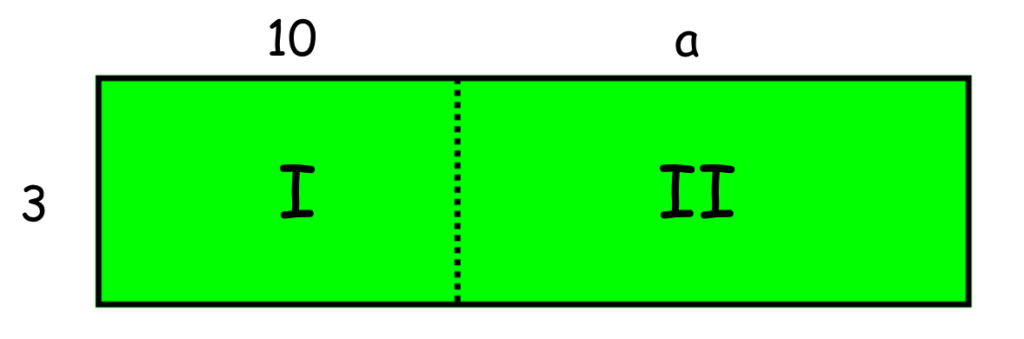
De lengte van de rechthoek is 3. De breedte van de rechthoek is de som van 10 en a dus:
De tegeltjes methode
De onderstaande rechthoek is d.m.v. twee stippellijnen verdeelt is vier stukken. De oppervlakte van de groene rechthoek is de som van de vier afzonderlijke oppervlakten.
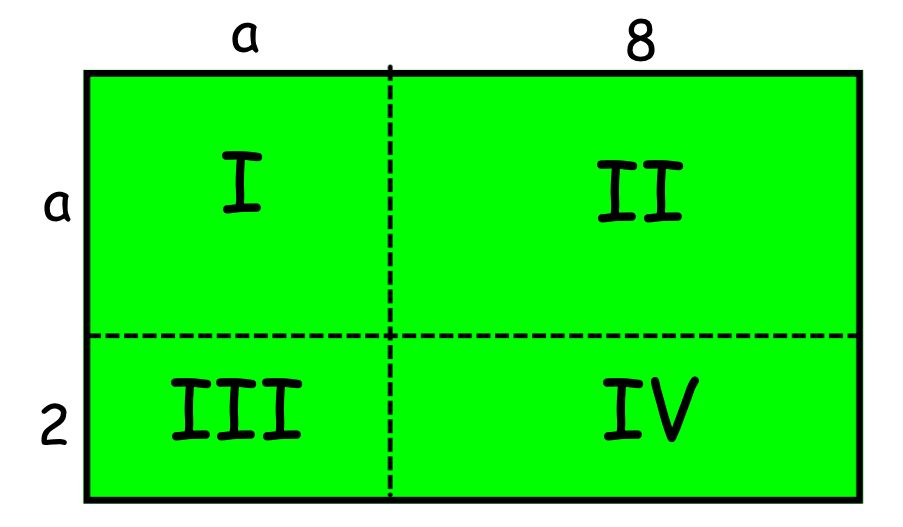
De lengte van de rechthoek is de som van a en 2 => (a+2) en de breedte van de rechthoek is de som van a en 8 => (a+8). Hieruit volgt de berekening:
Dubbele banaan of papegaaienbek methode
Als het bovenstaande voorbeeld met de tegeltjes goed bekijkt zie je dat je de beide termen die tussen de eerste haakjes staan vermenigvuldigt met de beide termen die tussen de andere haakjes staan. Hieronder stelt ieder boogje een vermenigvuldiging voor.
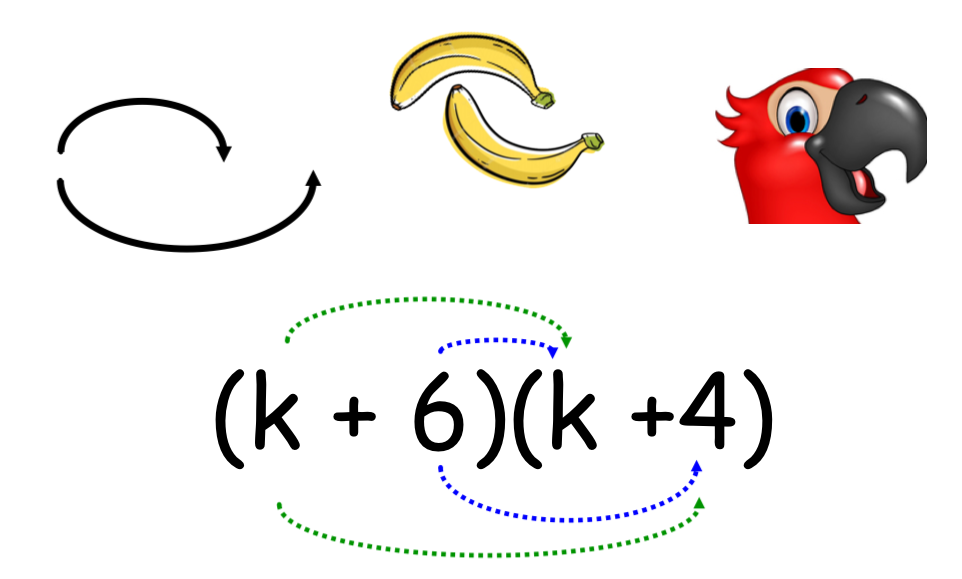
Met een beetje fantasie zie je dat de haakjes een dubbele banaan of een papegaaien bek vormen. Vandaar de naam

0 reacties