Inleiding
Op deze pagina lees je hoe je lineaire vergelijkingen kunt oplossen met de balansmethode. Deze oplossingsmethode kan je ook gebruiken bij 2e graad vergelijkingen alhoewel daar ook andere manieren voor zijn. Denk aan ontbinden in factoren of kwadraat afsplitsen. Druk op de groene knop als je direct naar de oefenopgaves wilt.
Een formule is een wiskundige zin waarin staat hoe je iets moet uitrekenen. Omdat je van te voren niet weet wat de uitkomst wordt van de formule, gebruik je voor de uitkomst een letter. Deze letter stelt dus een getal voor en kan elk willekeurig getal zijn.

De uitkomst van de formule hangt af van 'iets anders'. Voor dat iets anders wordt een tweede letter in de formule gebruikt. Ook deze letter stelt een getal voor.
Hiernaast zie je een voorbeeld van een formule waarmee je de kosten van een reparatie kunt uitrekenen. De reparatie kost 75,00 voorrijkosten plus 32,50 per uur. Voor een reparatie van twee uur ben je dus 140,00 kwijt. Je kunt dat uitrekenen door de u te vervangen door een '2'. Je krijgt dan
Zodra je van een formule een vraag maakt heb je te maken met een vergelijking.
Hoe lang duurt een reparatie als ik 205,00 moet betalen?
Bij deze vraag hoort de volgende vergelijking:
Bij een vergelijking is de uitkomst bekend. Je bent opzoek naar het getal wat je moet invullen op de plaats van de letter u zodat de uitkomst klopt.
Soms zie je de oplossing van eenvoudige vergelijkingen direct. Je kunt ook altijd een paar mogelijkheden proberen om te kijken of je de vergelijking kloppend krijgt. De meeste van jullie zien vast wel dat de oplossing van deze vergelijking a=10 is.
Door een paar waarden voor a in te vullen kom je al snel tot het antwoord
Kijk nog even goed naar de oplossing van de vergelijking. De oplossing is: a = 10. Zo zien alle oplossingen van vergelijkingen er uit: 'een letter' = 'een waarde'
Als de vergelijking wat lastiger is, en je ziet het niet direct, dan is de 'balansmethode' erg handig. Bij de balansmethode gaan we net zo vaak 'links en rechts" van de balans hetzelfde doen dat uiteindelijk de op lossing 'een letter' = 'een waarde' over blijft.
Voorbeeld 1
Hieronder is de vergelijking 2k+4=16 afgebeeld als een balans. Bij een vergelijking is het deel wat links van het '=' teken staat gelijk aan het deel aan de rechterkant. Zoals je ziet is de balans perfect in evenwicht. En dat willen we zo houden!
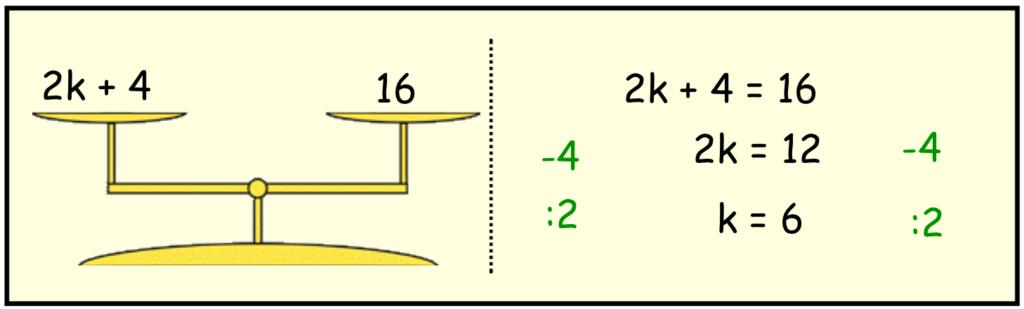
De oplossing van de vergelijking ziet er als volgt uit: k=..... Op de plaats van de puntjes komt een getal te staan. Aan de linkerkant van de balans willen we dus alleen een 'k' overhouden. Aan de rechter kant een getal.
Door aan de linker kant er 4 af te halen houd je 2k over: 2k +4 -4 = 2k. Maar dan moet ik dat rechts ook doen: 16-4 = 12. De nieuwe vergelijking wordt nu 2k=12. We willen naar 'k=....' Door 2k te delen door 2 houdt je k over. Maar dan moet je de rechter zijde ook door 2 delen. 12:2=6. Het antwoord is dus k=6
Voorbeeld 2
Dit voorbeeld bevat een vergelijking met aan beide zijde van het '=' tegen een letter. Ook nu is de oplossing k=....
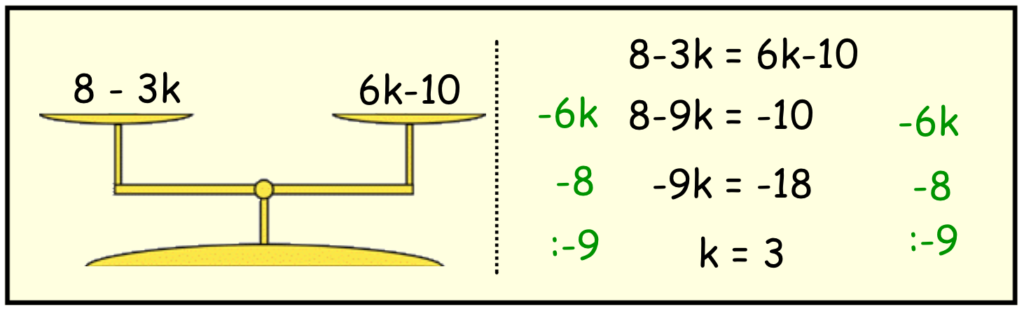
We starten door an de rechter kant de 6k weg te halen. Aan beide kanten van het '=' teken trekken we 6k af. Links: 8-3k-6k=8-9k, Rechts: 6k-10-6k=10. Nu halen we de acht weg aan de linker kant. Dat doen we door links en rechts 8 af te trekken. Links: 9-9k-8=-9k. Rechts: -10-8=-18. In de laatse stap delen we beide kanten door -9.

0 reacties